Know more about Free form surfaces

Common optical surfaces, including planar, spherical, rotationally symmetric aspheric, and cylindrical surfaces, do not fall under the category of freeform surfaces. By definition, a freeform surface is an optical surface that lacks rotational or translational symmetry constraints. Consequently, a significant characteristic of freeform surfaces is their asymmetry; they are not rotationally symmetric about any axis nor translationally symmetric about any plane.

Freeform surfaces were first applied in the field of illumination. With the development of single-point diamond turning technology, it became possible to manufacture molds for various surfaces. These molds can then be used in molding or injection molding processes to produce optical surfaces that meet specific requirements. Compared to traditional elements, freeform surfaces offer more degrees of freedom, enabling more compact designs, larger optical fields of view, and reduced system weight, thus enhancing the functionality of optical systems. In the field of optical imaging, freeform surfaces are widely used in astronomical observation and space optical systems. They are also incorporated into some smartphone lenses to correct aberrations.

A. Off-Axis Aspheric Surfaces

According to the definition of freeform surfaces, an off-axis segment of a rotationally symmetric aspheric surface, commonly referred to as an off-axis aspheric surface, falls under the category of freeform surfaces. The shape of an off-axis aspheric surface can be circular or rectangular.

An off-axis aspheric surface is derived from the original aspheric equation with the addition of an off-axis distance or angle parameter. It can be manufactured through CNC grinding and polishing.

B. Toroidal Surfaces

A toroidal surface, also known as a torus, resembles a segment taken from a car tire. It is curved in both the X and Y directions, with two different radii of curvature in two mutually perpendicular cross-sections. In optical systems, toroidal surfaces have unique applications, such as deformable optical elements in adaptive optics systems or scanning elements in infrared thermal imagers. In extreme ultraviolet spectrometers, toroidal surfaces can be used as pre-mirrors to collect more light flux. The shape of a toroidal surface is as follows:

Given the curvature radius in the horizontal X direction as ( R_x ) and the conic constant as ( K_x ), and the curvature radius in the horizontal Y direction as ( R_y ) and the conic constant as ( K_y ), the expression for a toroidal surface can be represented as:

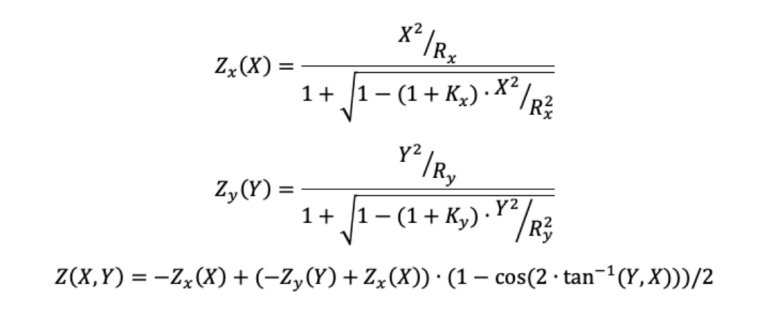
C. XY Polynomial Freeform Surfaces

XY polynomial surfaces are typically derived from aspheric surfaces by adding polynomial equations in x and y. The polynomial equations can be of any form, including linear, quadratic, cubic, and higher-order polynomials. These surfaces are controlled by multiple parameters, and by adjusting these parameters, different surface shapes can be obtained.

D. Zernike Polynomial Freeform Surfaces

In previous articles, we have detailed the concept of Zernike polynomials. The basis functions of Zernike polynomials are continuous, orthogonal, and complete within a unit circle. Each term corresponds to a form of aberration in optical testing, and the orthogonality ensures that the magnitude of each aberration coefficient is independent of the number of terms used in the fit. These properties make Zernike polynomials an ideal representation for freeform surfaces and are widely used in imaging optical design. The sag expression for a freeform surface with a diameter ( D ) obtained by superimposing Zernike polynomials on a quadratic surface is as follows:

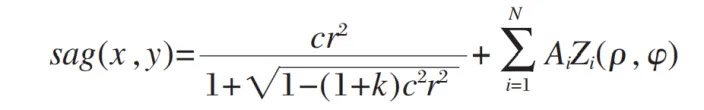
where the first term represents the quadratic surface, ( k ) is the conic constant, ( c ) is the curvature, ( r ) is the square root of the sum of the squares of x and y, the second term represents the Zernike polynomial, ( A_i ) are the Zernike polynomial coefficients, ( Z_i ) are the Zernike polynomials, ( \rho ) is the normalized radius ( r/(D/2) ), and ( \phi ) is the azimuthal angle.

E. Q Polynomial Freeform Surfaces

Q polynomial freeform surfaces were proposed by Forbes from QED Optics. These surfaces are derived from the rotationally symmetric Q polynomial surfaces proposed by Forbes. The surface coefficients can directly represent the sag deviation gradient relative to the best-fit sphere, which can be used for tolerance analysis of freeform surfaces. This allows for simultaneous evaluation of optical design and manufacturing difficulty, avoiding the cumbersome process of post-design manufacturing evaluation. The expression for Q polynomials is as follows:

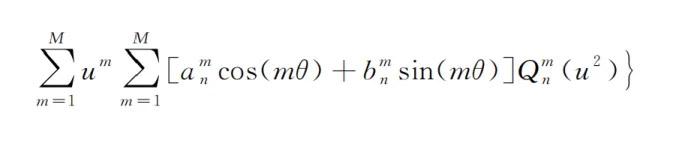
F. Non-Uniform Rational B-Splines (NURBS) Freeform Surfaces

NURBS surfaces describe surfaces through a network of control vertices, basis functions, and weights for each point. This is a parametric method for describing surfaces. NURBS is the only mathematical method defined by the International Organization for Standardization (ISO) for the geometric representation of industrial products in the STEP standard for data exchange. Adjusting each control point or its weight only affects the surface shape near that point, making NURBS a locally controllable freeform surface. The expression for NURBS surfaces is complex and is as follows:

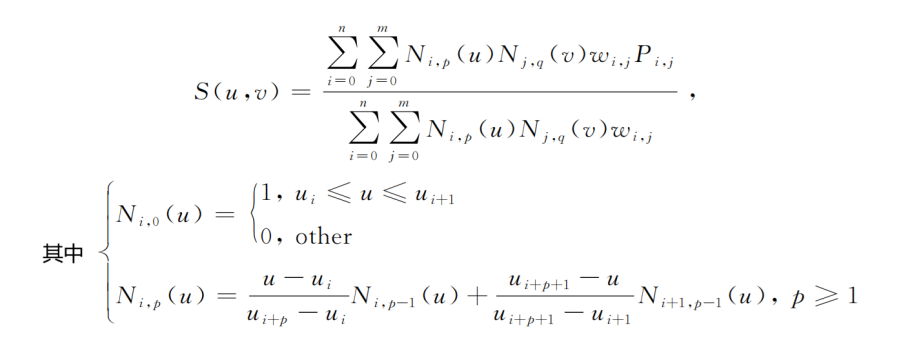
NURBS surfaces have excellent properties and have been successfully applied in the field of illumination. However, the large number of variables makes ray tracing extremely complex, time-consuming, and difficult to optimize, limiting their application in imaging fields.