Cylindrical Lens Considerations: Manufacturing, Errors, and Applications

Cylindrical lenses are similar to spherical lenses because both use curved surfaces to focus or diverge light. However, cylindrical lenses possess converging or diverging capabilities in only one direction and do not affect light in the perpendicular direction. This is something that cannot be achieved with spherical lenses, as they focus or diverge light in a rotationally symmetric manner. Cylindrical lenses play a crucial role in controlling and shaping laser beams, such as for laser sheet formation and circularizing elliptical beams. Due to the asymmetric nature of cylindrical lenses and the special manufacturing requirements, it is essential to specify and appropriately control centering, wedge, and axial twist.

Thus, cylindrical lenses require specialized equipment and techniques for manufacturing and a unique coordinate system to effectively reference the lens's characteristics. Two orthogonal directions define the reference system: the power direction and the non-power direction. The first direction, called the "functional direction," advances along the lens's curvature and is the only axis with optical functionality (Figure 1). The second direction, called the "non-functional direction," advances along the lens's length without any optical function. The length of the cylindrical lens can be extended along the non-functional direction without affecting the lens's optical function. Cylindrical lenses can come in various shapes, including rectangular, square, circular, and elliptical.

Errors, Aberrations, and Specifications

Figure 1: Functional and non-functional directions of rectangular and circular cylindrical lenses

Like any manufacturing process, imperfections are inevitable in the production of cylindrical lenses, leading to minor geometric errors. Improper calibration during polishing can result in mechanical errors specific to cylindrical lenses, causing optical distortions and negatively impacting performance. Therefore, strict control over these errors is necessary to ensure lens performance. These errors are defined according to geometric benchmarks, including the lens's flat side and the lens's edges.

Wedge

Figure 2 An example of wedge magnification caused by the difference in thickness between the two ends of a cylindrical lens in a non-functional direction

In an ideal cylindrical lens, the flat side of the lens is parallel to the cylindrical axis. The angular deviation between the flat side of the lens and the cylindrical axis is called wedge, typically measured in arcminutes (Figure 2). This angle is determined by measuring the thickness at both ends of the lens and calculating the angle between them. Wedge causes image shift in the non-functional direction, similar to the effect of wedge in a windowpane.

Co-axiality

Figure 3: An example of a coaxiality error caused by a difference in edge thickness in the functional direction of a cylindrical lens

In an ideal cylindrical lens, the optical axis of the curved surface is parallel to the lens's edge (Figure 3). The co-axiality error of a cylindrical lens is the angular displacement of the optical axis relative to the lens's edge, similar to the eccentricity of optically functional surfaces in spherical optical elements. This co-axial angle (α) causes the optical and mechanical axes of the lens to no longer be collinear, leading to beam shift. If the lens's edge is used as a mounting reference, this error makes optical alignment very difficult. However, if the lens's edge is not relied upon as a mounting reference, this error can be mitigated by offsetting the lens in the correct direction. The larger the diameter of the cylindrical lens, the greater the associated edge thickness difference for a given co-axial angle.

Axial Twist

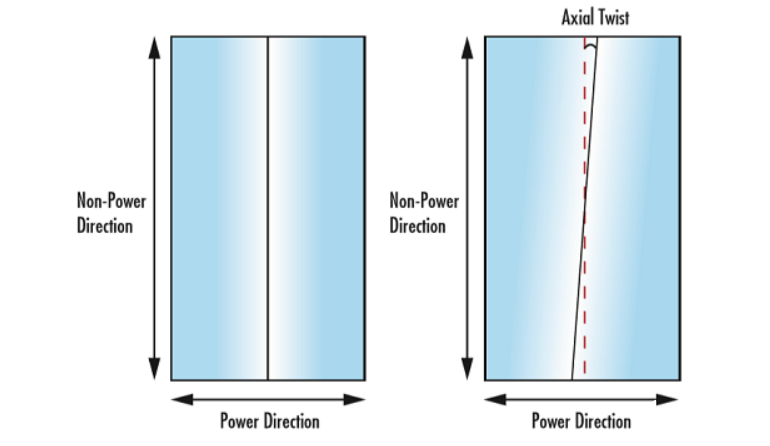
Figure 4: Example of axial torsion in a cylindrical lens

Axial twist is the angular displacement between the cylindrical axis and the lens's edge. Axial twist represents the rotation of the functional surface of the cylindrical lens relative to the outer diameter, causing the image to rotate around the optical plane. This is particularly detrimental in applications where a rectangular outer surface is fixed by its outer dimensions (Figure 4). Rotating the cylindrical lens to align the cylindrical axis can counteract axial twist.

Cylindrical lenses are most commonly used in laser beam shaping to correct asymmetric beams, create laser lines, or generate laser sheets. Modern scientific methods, such as particle image velocimetry (PIV) and laser-induced fluorescence (LIF), often require a thin laser line or a uniform laser sheet. Structured laser light is also a critical tool in scanning, measurement, and calibration applications. Low-cost laser diodes are now readily available, leading to another common application: simply circularizing the elliptical output of the diode to create a collimated and symmetric beam.

A laser sheet is a beam that diverges in both the X and Y axes. The laser sheet includes a rectangular field orthogonal to the optical axis, extending as the propagation distance increases. A laser line produced using a cylindrical lens can also be considered a laser sheet, although this sheet is triangular and extends along the optical axis.

To create a true laser sheet with two divergent axes, a pair of orthogonally oriented convex and concave cylindrical lenses is required (Figure 5). Each lens acts on a different axis, and the combination of the two lenses generates a divergent laser sheet.

Figure 5: Example of an orthogonal cylindrical lens used to generate a rectangular light plate

Without collimating optics, a laser diode will diverge in an asymmetric fashion. Spherical optical elements cannot produce a circular collimated beam because the lens acts on both axes simultaneously, maintaining the original beam's asymmetry. A pair of perpendicular cylindrical lenses can handle each axis individually.

To produce a symmetric output beam, the focal length ratio of the two cylindrical lenses should match the ratio of the X and Y beam divergences. Similar to standard collimation, placing the diode at the focal point of the two lenses, with the distance between the lenses equal to the difference in their focal lengths (Figure 6).

Figure 6: An example of toroidal elliptic beams using cylindrical lenses

The divergence of a laser diode can be quite large, which can present challenges when attempting to collimate, as the divergence directly impacts the system's allowable length and the required lens size. The focal length fixes the relative positions of each component, so the maximum beam width (d) for each lens can be calculated using the lens's focal length (f) and the divergence angle (θ). Therefore, the clear aperture of each lens must be larger than the corresponding maximum beam width.