Reflective optical systems are widely used in various fields today, primarily due to their ability to avoid chromatic aberration while achieving high imaging quality. Compared to refractive systems, reflective systems use mirror reflection instead of lens refraction, featuring fewer optical elements and higher optical performance stability. This article will explore the basic structure, characteristics, and optical properties of reflective systems in different environments. We hope this article will be helpful to our readers.
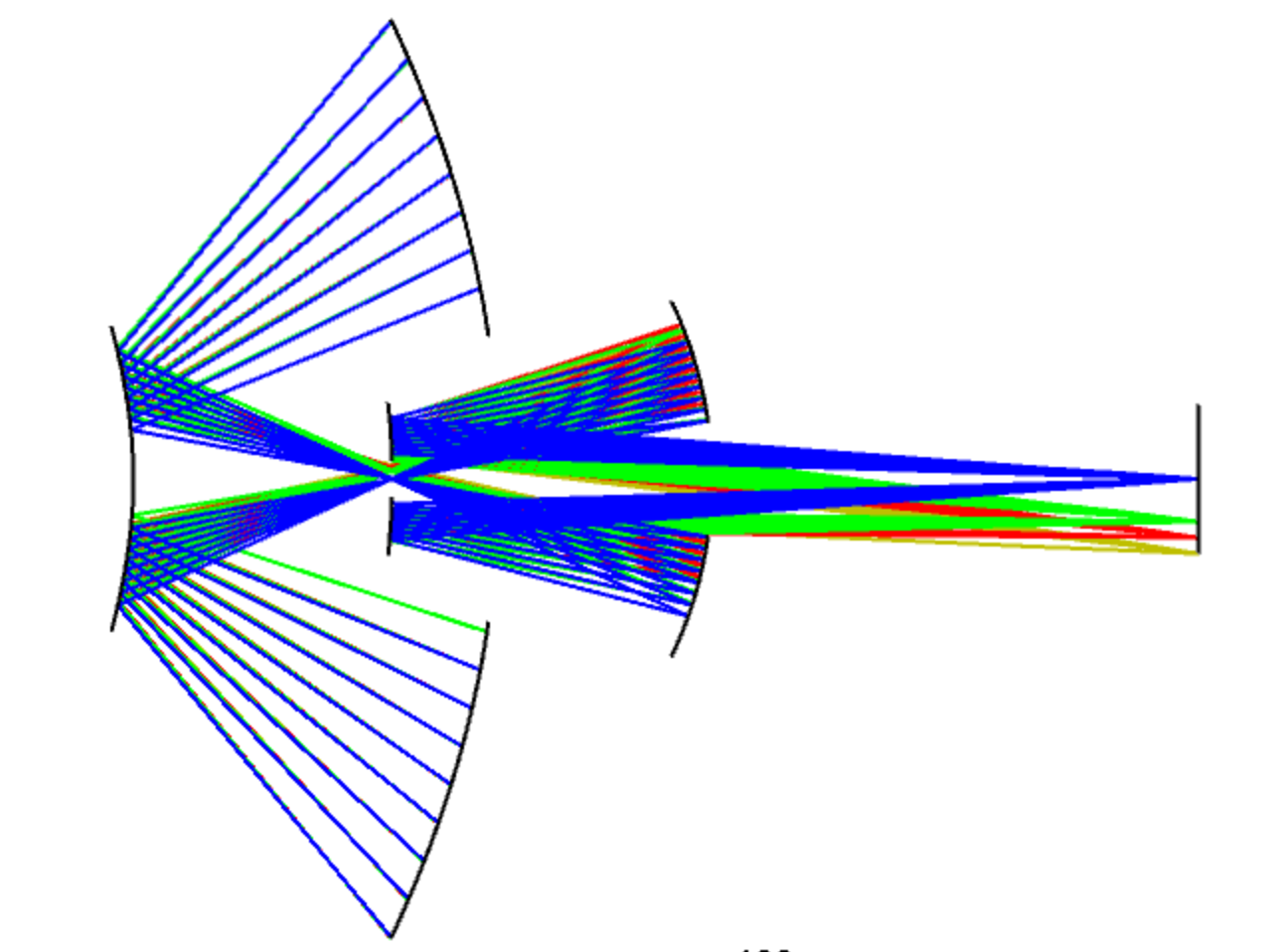
The Schmidt optical system is a common type of reflective optical system, mainly used in astronomical telescopes and other high-precision imaging devices. The key to its design lies in the use of a Schmidt corrector plate, which effectively corrects spherical aberration, thereby improving imaging quality. The basic structure of a Schmidt optical system includes a spherical primary mirror and a Schmidt corrector plate, which is usually placed at the center of curvature of the primary mirror.
Aspheric optical elements from the aspheric lenses manufacturers play a crucial role in reflective optical systems. Aspheric mirrors can effectively correct aberrations and improve imaging quality. Modern manufacturing techniques, such as single-point diamond turning, have made the production of large-diameter aspheric mirrors more feasible. These technological advancements have broadened the application of reflective optical systems in high-precision imaging fields.
From the perspective of light transmission, there are fundamental differences between lens systems and mirror systems. In lens systems, light often passes directly through and utilizes the entire aperture of the entrance pupil. In contrast, mirror systems inherently differ as mirrors may obstruct each other, as seen in the classic dual-mirror Cassegrain system. This characteristic can lead to a noticeable drop in the MTF (Modulation Transfer Function) curve at mid-frequencies.
Reflective systems have certain advantages over refractive systems. Firstly, according to Snell’s law, the refractive index for all wavelengths can be considered -1 for mirrors, allowing reflective systems to avoid chromatic aberration. This makes them particularly effective in large-aperture and wide-angle designs. Secondly, reflective systems generally require fewer optical elements, reducing manufacturing costs and maintenance difficulty. Since the mirror surface is not constrained by optical materials, reflective systems can achieve large apertures, which is crucial in fields like astronomy and aerospace. Additionally, the design freedom of mirrors is higher, with freeform surfaces being a popular research direction.
Reflective systems, aside from central obstructions, also face mutual interference between mirrors, significantly increasing alignment difficulty. Supporting structures and other mechanical components further add to the system’s compactness, often resulting in fewer optical elements. The issues of light blocking and component interference limit the field of view of reflective systems. With limited elements, it becomes challenging for reflective systems to avoid using aspheric surfaces to control aberrations. The most primitive reflective optical system is the Newtonian system, where the spherical primary mirror keeps almost only the on-axis points clear.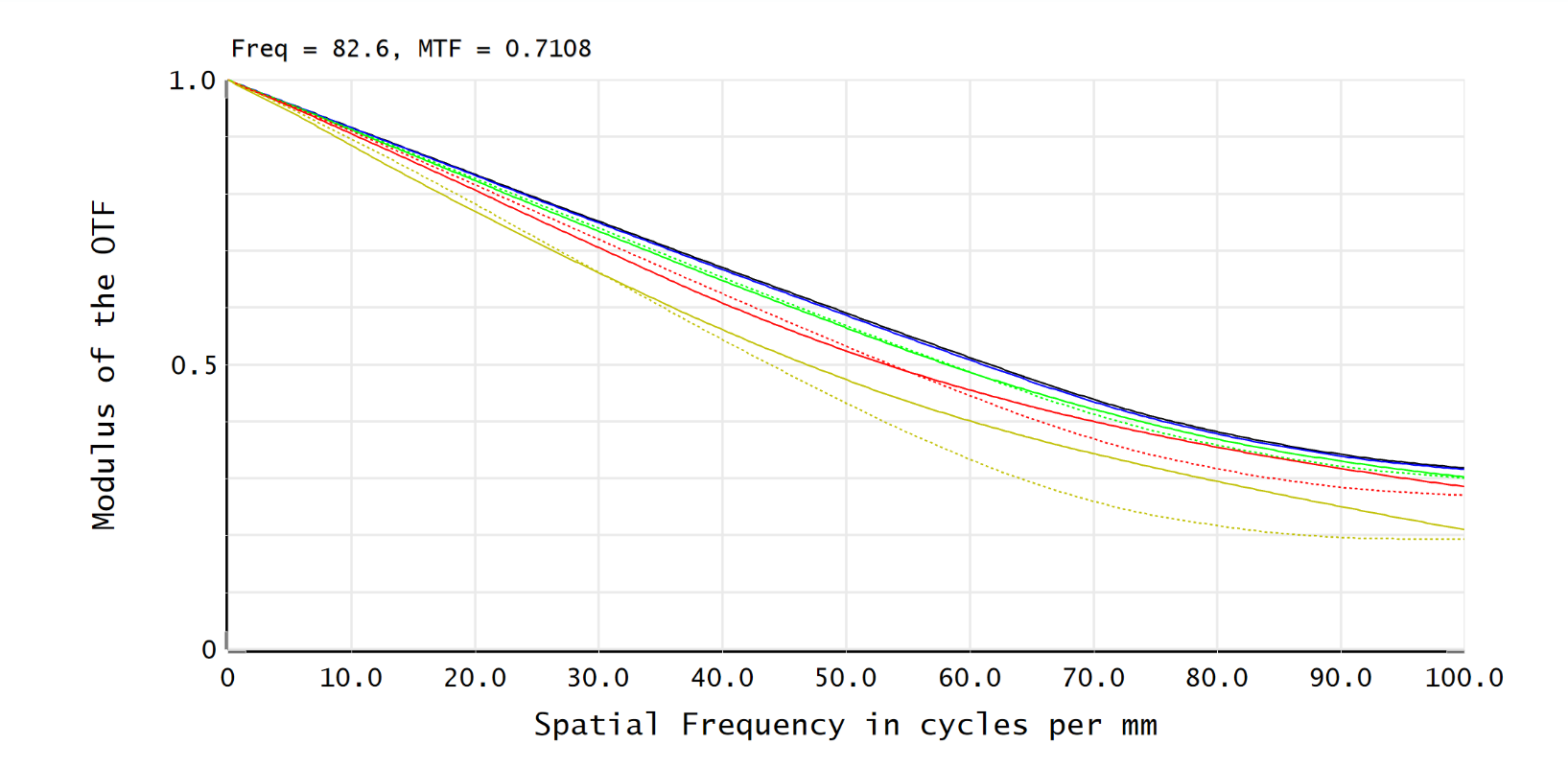
The thermal characteristics of reflective optical systems are primarily determined by the thermal expansion coefficient of their materials. If a reflective system is made of a single material, such as aluminum, its thermal effects are usually negligible. This is because, under uniform temperature changes, the entire system expands or contracts uniformly. Since all system parameters (such as mirror curvature) scale proportionally, no aberrations occur, and imaging remains clear. However, in practical applications, reflective systems may require multiple materials, making thermal gradient effects significant. When different materials have different thermal expansion coefficients, or when there are temperature differences within the system, thermal gradients can cause different parts to expand or contract differently, affecting the system’s optical performance. In such cases, imaging may exhibit aberrations or distortions, especially in environments with large temperature variations, potentially affecting image quality stability. Therefore, for reflective systems using multiple materials or experiencing thermal gradients, careful evaluation of thermal characteristics is essential. Designers need to consider the thermal expansion coefficients of materials, the impact of temperature changes on system parameters, and the potential effects on imaging quality. Through precise thermal analysis, these thermal effects on optical performance can be predicted and minimized.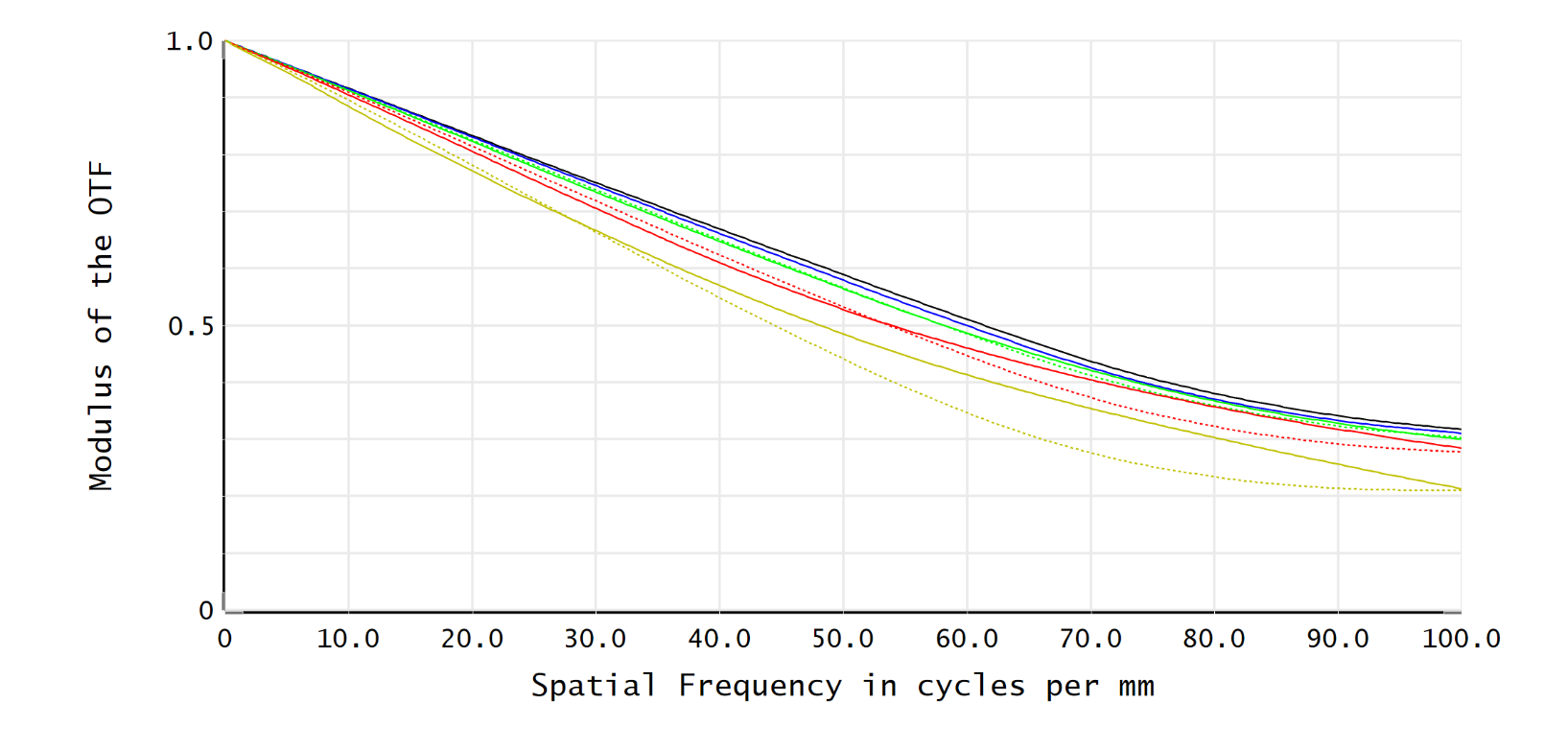
For catadioptric systems, to address the aforementioned thermal expansion issues, many high-precision mirrors use materials like Zerodur. Zerodur has an almost zero thermal expansion coefficient, allowing it to maintain stable dimensional changes under temperature variations. Therefore, Zerodur is widely used in large-diameter mirrors, especially in astronomical telescopes and other high-precision optical systems. Reflective systems using this material can maintain good optical performance in environments with significant temperature changes, avoiding aberrations caused by thermal expansion.