Differences Between Spherical and Aspherical Optics

Differences Between Spherical and Aspherical Optics
Geometric Shapes, Advantages, and Applications of Spherical and Aspherical Optics

One of the most commonly used lens shapes in the optical market remains the spherical lens. Due to mature design and precise manufacturing capabilities, it meets high optical quality standards. At the same time, economical and high-precision production of aspherical lenses is also feasible. Thanks to advancements in cutting-edge technology, the use of aspherical lenses in modern systems—such as medical technology or laser material processing—has become possible. To this day, the production of both types of lenses can be further optimized through sophisticated CNC technology, intelligent control software, and interferometry. The primary differences between spherical and aspherical lenses lie in their geometric shapes as well as the complexity of their production and measurement.

Spherical Lenses

Spherical lenses are rotationally symmetric optical elements whose shape corresponds to a section of a spherical surface (Figure 1). The radius of curvature remains constant relative to the geometric center. This means the optically effective surface can be described by specifying just one parameter—the radius (R). Since this parameter is consistent across the entire surface, spherical lenses offer cost advantages in manufacturing.

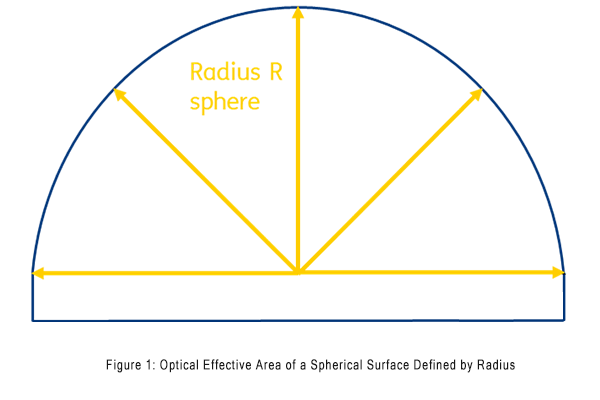
Manufacturing Advantages of Spherical Lenses

Spherical lenses offer significant cost advantages in production due to their geometric simplicity. The uniform curvature of spherical surfaces enables straightforward manufacturing processes and shorter production times, especially for smaller diameters, where multiple optical elements can be fabricated simultaneously on a single substrate.

This simplicity also extends to optical inspection and metrology. The consistent curvature allows for rapid and uniform measurements across the entire surface. Both tactile measurement methods (e.g., profilometers or 3D coordinate measuring machines) and optical techniques (e.g., interferometers and computer-generated holograms, CGH) can be efficiently applied to assess spherical surfaces.

As with all optical components, the choice of measurement method depends on a cost-benefit analysis to determine the most suitable approach for quality control. The combination of manufacturability and ease of verification makes spherical lenses a cost-effective solution for many applications.

Application Fields of Spherical Lenses
Spherical lenses find extensive applications across various domains, such as metrology, aerospace (spectrometers installed inside satellites), and medical technology (slit lamps for anterior eye segment examination). With their low manufacturing costs, short production cycles, and broad optical applications, spherical lenses remain an indispensable component in the optical market, offering excellent cost-performance ratio.

Optimization of Spherical Single Lens Applications

Based on their shape, spherical lenses utilize their light-converging, diverging or focusing properties to refract incident light to desired diopter levels. In imaging systems, for instance, achieving high image quality is paramount while minimizing optical aberrations. The image quality can be further enhanced by considering various parameters tailored to specific system requirements.

Key optimization factors include:

1. Light source positioning

2. Selection of effective aperture

3. Lens shape configuration

4. Spatial constraints of the optical system

Aperture optimization proves particularly effective in reducing spherical aberration. This occurs because:

· The aperture blocks peripheral incident light rays

· Unrestricted apertures allow increased curvature at edges

· Stronger refraction at periphery exacerbates spherical aberration

The strategic use of multiple spherical lenses can also improve performance, though this approach must balance:

· Lens shape combinations

· Available system space

· Overall optical path requirements

This optimization approach demonstrates how spherical lenses can be fine-tuned for specific applications while maintaining their inherent manufacturing advantages.

Cemented spherical lens

Cemented spherical lenses create achromatic doublets by combining one or more converging and diverging lenses. Typically, a low-refractive-index positive convex lens (crown glass) and a high-refractive-index negative concave lens (flint glass) are bonded together, thereby improving both spherical aberration and chromatic aberration in optical systems. For instance, in photography, achromatic lenses are commonly used in camera lenses.

Aspherical Lenses

When various factors must be considered in optical devices—such as high image quality, numerical aperture, or maximum space savings—aspherical lenses become the optimal choice. An aspherical lens is a rotationally symmetric optical element whose radius of curvature deviates radially from the lens center. Due to this unique surface geometry, aspherical lenses can significantly enhance the imaging quality of optical systems compared to spherical lenses. Their varying radii of curvature result in deviations from spherical surfaces (Figure 2).

A closer observation of the flattened radius towards the lens periphery reveals a more noticeable deviation from spherical curvature. Generally speaking, the following principle applies: when a radius deviates from spherical, it is considered aspherical.

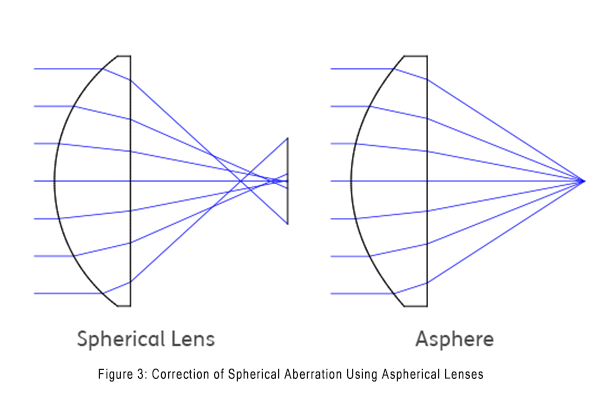
As illustrated in Figure 3, the lens radius is designed in such a way that incoming light beams intersect at a common focal point, thereby preventing spherical aberration. Thus, aspherical lenses represent optimized focusing optical elements.

In contrast, with spherical lenses, incident light rays exhibit greater deflection as their distance optical axis increases, failing to converge at a single point (Figure 3). This spherical aberration results in slightly blurred, less sharp images. Therefore, aspherical lenses can be employed to enhance image quality.

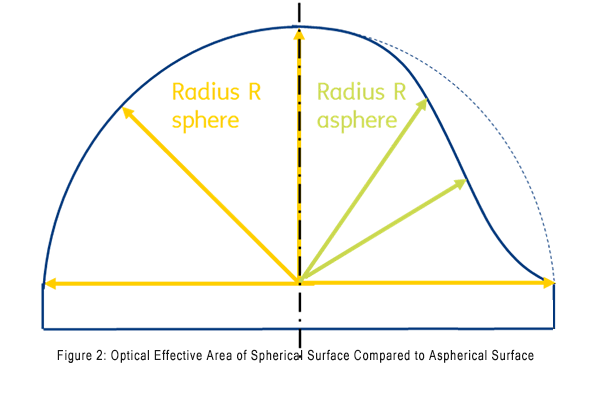
Upon closer examination of the flattened radius at the lens periphery, the deviation from spherical curvature becomes evident. The fundamental principle states: any lens whose radius deviates from spherical is aspherical.

As depicted in Figure 3, the lens radius is specifically designed to make incident light beams converge at a common focal point, thereby eliminating spherical aberration. This makes aspherical lenses optimized focusing elements.

In contrast, spherical lenses exhibit progressively greater deflection of incident light with increasing distance from the optical axis, preventing convergence at a single point (Figure 3). The resulting spherical aberration produces slightly blurred images. Thus, aspherical lenses effectively enhance image quality.

Mathematical Description of Aspherical Surfaces

In terms of optical design, aspherical surfaces offer greater degrees of freedom compared to spherical surfaces, enabling the creation of more complex surface profiles. The optically effective surface of a rotationally symmetric aspherical lens is conventionally defined by the following aspheric equation:

[Note: This would typically be followed by the standard aspheric formula:
z(h) = (ch²)/[1+√(1-(1+k)c²h²)] + Ah⁴ + Bh⁶ + Ch⁸ + Dh¹⁰ + ...
where:
z = surface sag
h = radial distance from optical axis
c = curvature (1/radius)
k = conic constant
A,B,C,D = aspheric coefficients]

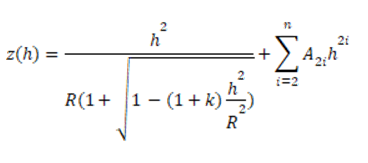
If the aspheric coefficients are zero, the surface profile corresponds to a rotationally symmetric conic section. This can be expressed as follows:

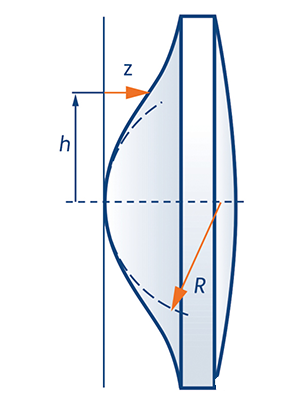
Since the 2015 update to ISO 10110, an alternative mathematical description has been introduced for characterizing aspherical surfaces. This method utilizes a set of orthogonal polynomials known as Qbfs (Q-type best-fit sphere) polynomials, which model surface deviations relative to an aspheric surface's optimal reference sphere. The surface profile is defined by the following formula:

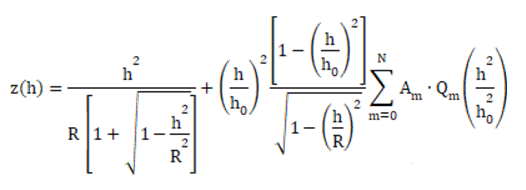
The new description offers significant advantages, requiring fewer significant figures to accurately characterize surface profiles. Additionally, the maximum deviation can be efficiently estimated by multiplying the largest coefficient Am by the maximum amplitude of its corresponding polynomial order (see Figure 4).

Optical System Simplification Using Aspheric Lenses

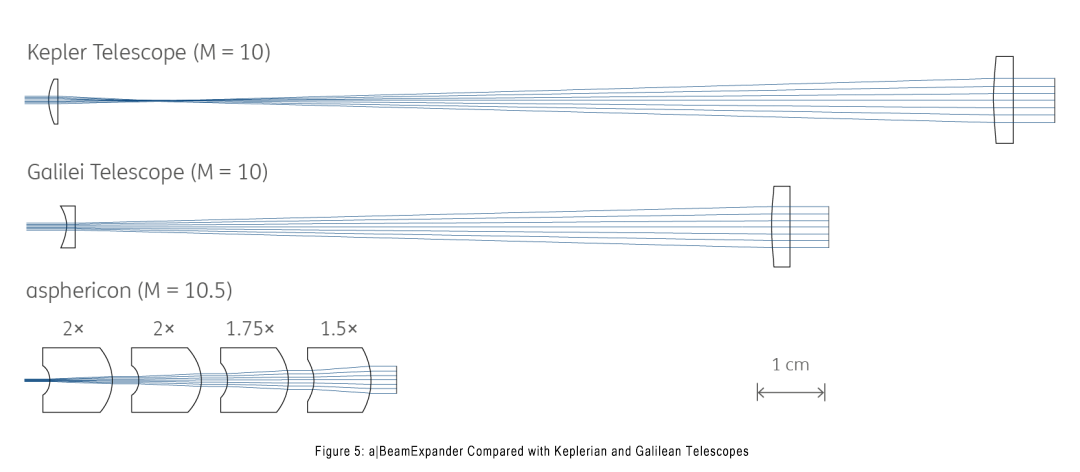
Compared to conventional lenses, aspheric lenses offer the additional advantage of reducing overall system length. A prime example is the monolithic beam expander developed by Bena Optics for beam expansion applications.

Key features include:

1. Afocal system implementation using just one lens, achieved by aspherizing one surface of a two-lens configuration

2. Capability for large-diameter beam expansion without aperture errors

3. Modular design allowing multiple units to be connected in series

The Bena Optics a|BeamExpander system demonstrates:

· 50% reduction in total length compared to traditional systems

· Equivalent 10× magnification (M=10) at half the length of comparable Keplerian or Galilean telescope configurations

(The accompanying illustration would typically show:
a) Conventional 10× beam expander dimensions
b) Compact a|BeamExpander design
c) Performance comparison between both systems)

This innovation highlights how aspheric optics enable:
✓ More compact optical configurations
✓ Flexible system scalability
✓ Enhanced performance in space-constrained applications

Aspheric Lens Manufacturing and Metrology

Like spherical lenses, aspheric lenses can be produced through various methods, including grinding and polishing. For a long time, it was believed that aspheric lenses were only suitable for laboratory use, R&D projects, or prototype development, with mass production considered economically unviable. However, modern manufacturing and measurement technologies now enable reproducible, high-precision mass production of aspheric lenses. Increased production volumes help distribute setup costs, ultimately reducing per-unit pricing.

Globally, Bena Optics' fully digitalized production process is unparalleled. Every step—from initial customer contact to final shipment of the optical system—is digitally controlled using proprietary, software-based management tools (Figure 6). This approach significantly optimizes production workflows, improves yield through streamlined data analysis (target vs. actual), and ensures lossless data transfer. The system also supports:

· Increasing automation in manufacturing

· Digital control of supplier and logistics processes

Expanded Manufacturing Capabilities and Advanced Metrology

The high flexibility in tool selection has significantly broadened the range of achievable optical geometries, thereby reducing the cost of aspheric lenses. Beyond material selection and diameter specifications, the primary cost drivers are:

· Surface form deviation

· Surface quality requirements

Recent advancements have streamlined aspheric lens metrology:

1.Enhanced Conventional Methods

2.Computer-generated holography (CGH) - Interferometry

Tactile probe measurements

3.Innovative Techniques

4.Tilt-wave interferometry: Measures optical surfaces in 20-30 seconds using multiple tilted wavefronts

Sub-aperture stitching: Non-contact acquisition of surface data from multiple zones, reconstructed into full topography

Deviation mapping: Automated comparison against target specifications

These developments enable:
✓ 80% faster measurement cycles
✓ Sub-micron form accuracy verification
✓ Real-time production feedback

(Visualization would typically show wavefront analysis and 3D deviation heatmaps, demonstrating metrology efficiency gains.)

The synergy between advanced manufacturing and precision metrology now makes aspheric lenses economically viable for commercial applications.

Applications of Aspheric Lenses

Thanks to their ability to correct spherical aberration, aspheric lenses are widely used in various fields, including metrology, imaging, and laser applications (see the example of laser beam expansion in the section "Optical System Miniaturization Using Aspheric Lenses"). For instance, they enhance the optical performance of modern fluorescence microscopes, projection systems, and laser setups.

A key advantage of replacing spherical lenses with aspheric lenses in optical systems is the significant reduction in system size and weight—a critical factor in industries such as aerospace. For example, weight reduction in Earth observation satellites can substantially decrease fuel consumption during launch.

Key Benefits in Applications:

1. Compact & Lightweight Designs – Ideal for portable devices and aerospace systems

2. Improved Optical Performance – Sharper imaging, reduced aberrations

3. Energy Efficiency – Lower fuel costs in satellite launches due to reduced payload weight

4. Versatility – Suitable for high-precision microscopy, laser focusing, and projection optics

Comparison of Spherical vs. Aspherical Lenses

While aspherical lenses offer superior imaging quality, their advantages come with more complex manufacturing and metrology requirements, resulting in higher costs compared to spherical lenses. However, these costs can be offset by system-level savings when replacing multiple spherical lenses with a single aspherical element.

The table below compares key geometric and performance characteristics of both lens types:

Key Trade-offs:

· Performance vs. Cost: Aspherical lenses provide better aberration control but at higher production costs

· System Complexity: Fewer elements needed with aspherical designs, reducing overall size/weight

· Economic Viability: Mass production improves cost efficiency for aspherical lenses

The above content is sourced from the internet. If any infringement occurs, please notify us and it will be removed.